用户注册

年金终值、年金现值、这两个是资金时间价值计算必备的知识点，几乎所有的职业资格考试都会涉及，我们需要知道怎么推理出这个公式，就明白了如何运用到实际中，对这个公式有点晕乎的同学们就跟着会计教练的小编一起来看看这篇年金现值和年金终值的公式怎么推导的文章。

年金终值、年金现值、这两个是资金时间价值计算必备的知识点，几乎所有的职业资格考试都会涉及，我们需要知道怎么推理出这个公式，就明白了如何运用到实际中，对这个公式有点晕乎的同学们就跟着会计教练的小编一起来看看这篇年金现值和年金终值的公式怎么推导的文章。

年金现值和年金终值的推导公式

例子：

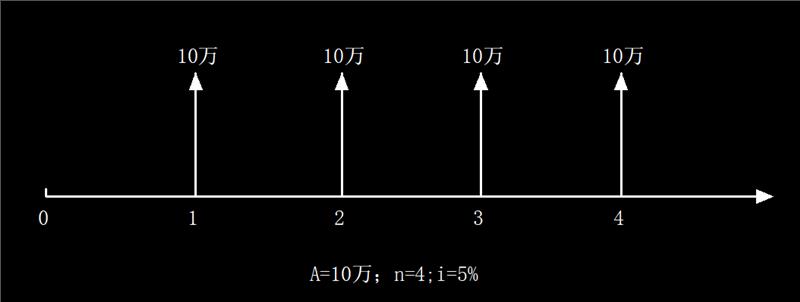
现金流量图

以图示现金流量图为例，每期存入银行A=10万元，利率i=5%，到第四期末本利和F为多少？

年金终值（F/A,i,n）推导过程：

1、以复利的方式计算，这一步过程是推导的基础，年金终值公式正是在这个基础上化解出来的：

F=A*(1+i)^3+A*(1+i)^2+A*(1+i)^1+A=A*【(1+i)^3+(1+i)^2+(1+i)^1+1】

=10*【(1+5%)^3+(1+5%)^2+(1+5%)^1+1】

2、【(1+i)^3+(1+i)^2+(1+i)^1+1】是一个等比数列，且公比q=（1+i）=(1+5%)，所以数列和Sn=(1-q^n)/(1-q)，将q替换成（1+i），则Sn=[1-(1+i)^n]/[1-(1+i)]=[(1+i)^n-1]/i

3、结合1和2，则F=A*[(1+i)^n-1]/i=10*[(1+5%)^4-1]/5%，反之A=F* i/[(1+i)^n-1]。

年金现值（P/A,i,n）推导过程

根据F=A*[(1+i)^n-1]/i和F=P(1+i)^n，可知A*[(1+i)^n-1]/i=P(1+i)^n，

所以A=P* i(1+i)^n/[(1+i)^n-1];P=A*[(1+i)^n-1]/i(1+i)^n。

增长型年金现值的计算

例4：某教育基金打算为山区小学提供20年的教育补助，年末支付给山区小学10万元，并且该资金以每年5%的增长率增长，比如第2年年末需要支付10.5万，而该教育基金的投资回报率（贴现率）为10%，那么请问该教育基金目前需要准备多少钱？

该题案例属于增长型年金求现值，可以代入相应的公式（公式的推导这就不阐述了）。

其中公式C为第1年支付金额，r为投资回报率，g为年金增长率，t为支付期限，公式表现为两种形式：

当r≠g；PV=C/(r-g)*{1-[(1+g)/(1+r)]^t}

当r=g；PV=t*C/(1+r)

因为题文r≠g，所以将数值代入公式PV=C/(r-g)*{1-[(1+g)/(1+r)]^t}=121.2080万元。

这么难记的公式谁去记它？所以，要求该现值，我们可以反推回去，通过Excel普通年金求得第二年现值，再求得当前现值。

这里需要分三步来走：

1、求第二年年末支付金额：10万*105%=10.5万。

2、求第二年年初现值（将增长年金转为普通年金）：因为投资回报率为10%，而支付增长率为5%，那么一边按比例流入，一边按比例流出，相较于本金而言，实际投资回报率为r-g=10%-5%=5%（类同以对冲掉通货膨胀率后的实际收益率）。也就是说，从第2年到第20年就变成类同于养老金的领取（如上文Excel的PV函数求得），在未来的19年中，由增长型年金转化为普通年金，那么第2年年初的现值（或需要准备的资金，如下图求得）为1332407元。

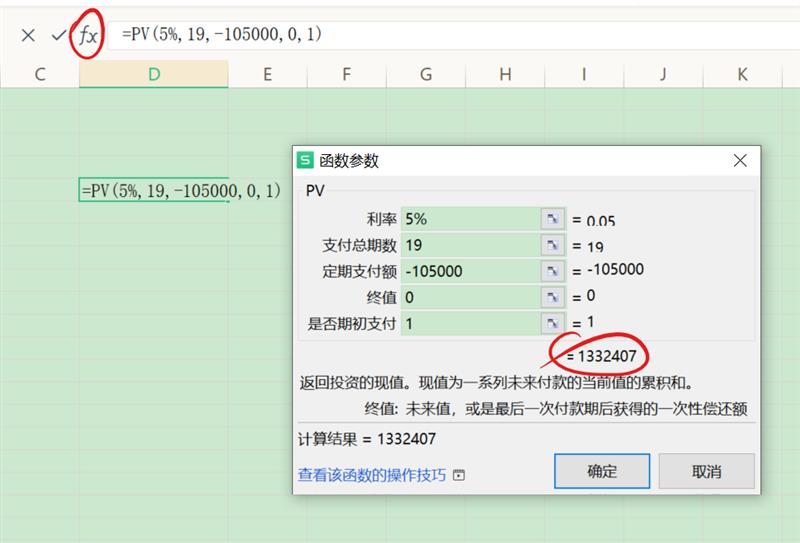
3、求当前现值（第1年年初现值）：因为支付是期末支付（或者说第2年年初支付，第1年年末的终值等于第2年年初的现值），而第1年年末相较于年初已经通过投资获得10%的收入，那么根据FV=PV*(1+r)的公式，PV=FV/110%=1332407/110%=121.1208万，与前文的计算结果是一致的。

看完以上关于年金现值和年金终值的公式怎么推导，大家应该知道了这个公式如何演算，后续还有相关的案例分析，是关于增长型年金现值的计算方法，希望可以帮助大家理解该知识点，还有什么不明白的地方，随时可以联系我们会计教练的老师咨询，还可以点击下方的链接免费领取零基础会计实操资料包!

叮!免费赠送!零基础会计实操资料包!